Математика учит, как вычислять размеры основных геометрических фигур. Простые формулы пригодятся в учебе. Умение рассчитать площади разных фигур имеет практическое применение.
Площадь прямоугольника
Площадью геометрической фигуры принято считать пространство на плоскости, заключённое в пределах периметра или границы данной фигуры. Для вычисления площади основных геометрических фигур применяют специальные формулы, которые следует запомнить. В формулах площадь обозначается заглавной латинской буквой S, а единицей площади считают квадрат единиц длины — мм², см², м², км².
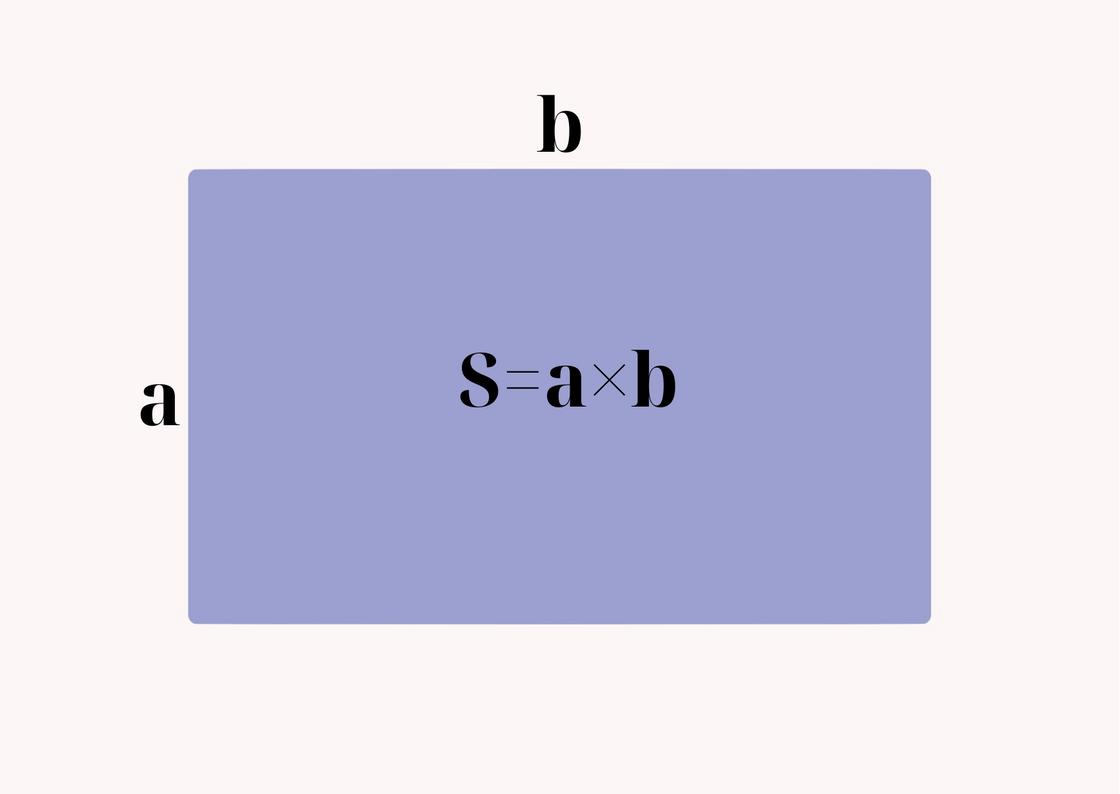
Прямоугольник — это геометрическая фигура, созданная четырьмя отрезками ломаной линии. Он состоит из четырёх сторон, соединенных под прямыми углами. Противоположные стороны прямоугольника параллельны и равны по длине. То есть у прямоугольника АВСD AB=CD, BC=AD.
Как найти площадь прямоугольника? Площадь прямоугольника равна произведению его длины на ширину: S=а×b, где S — площадь, а и b — смежные стороны прямоугольника. Если в задаче сторона а=10 см, а сторона b=5 см, то S=10×5=50 см², то есть площадь данного прямоугольника составляет 50 см².
Есть множество разнообразных фигур, составленных прямоугольниками разных размеров. На сайте крупнейшего в мире издателя образовательных ресурсов Twinkl даны примеры вычисления сложных составных фигур из разных прямоугольников.
Площадь квадрата
Квадратом называется четырёхугольник, все стороны которого равны и соединены под прямыми углами. Как найти площадь квадрата? Для её вычисления есть несколько способов и формул в зависимости от того, что о нём известно:
- Если в задаче дана длина стороны квадрата, то можно применить две формулы: S=a×a или S=a², где a — сторона квадрата. Если дана сторона квадрата 4 см, то его площадь вычисляйте так: S=4×4=16 см² или S=4²=16 см².
- Если известна только диагональ квадрата, площадь можно вычислить по формуле S=d²÷2, где d — диагональ. Например, если d=6 см, то S=6²÷2=36÷2=18 см².
- Если дана длина периметра квадрата, то площадь его вычисляется по формуле S=P²÷16, где Р — периметр квадрата. Например, дано Р=20 см, тогда S=20²÷16=400÷16=25 см².
Вычислить площадь квадрата по известному периметру можно другим способом: сначала нужно узнать длину одной стороны, разделив периметр на 4, так как 4 стороны квадрата равны: 20÷4=5 см. Затем вычислить площадь по формулам S=a×a или S=a², получим S=5×5=25 см² или S=5²=25 см².
Площадь параллелограмма
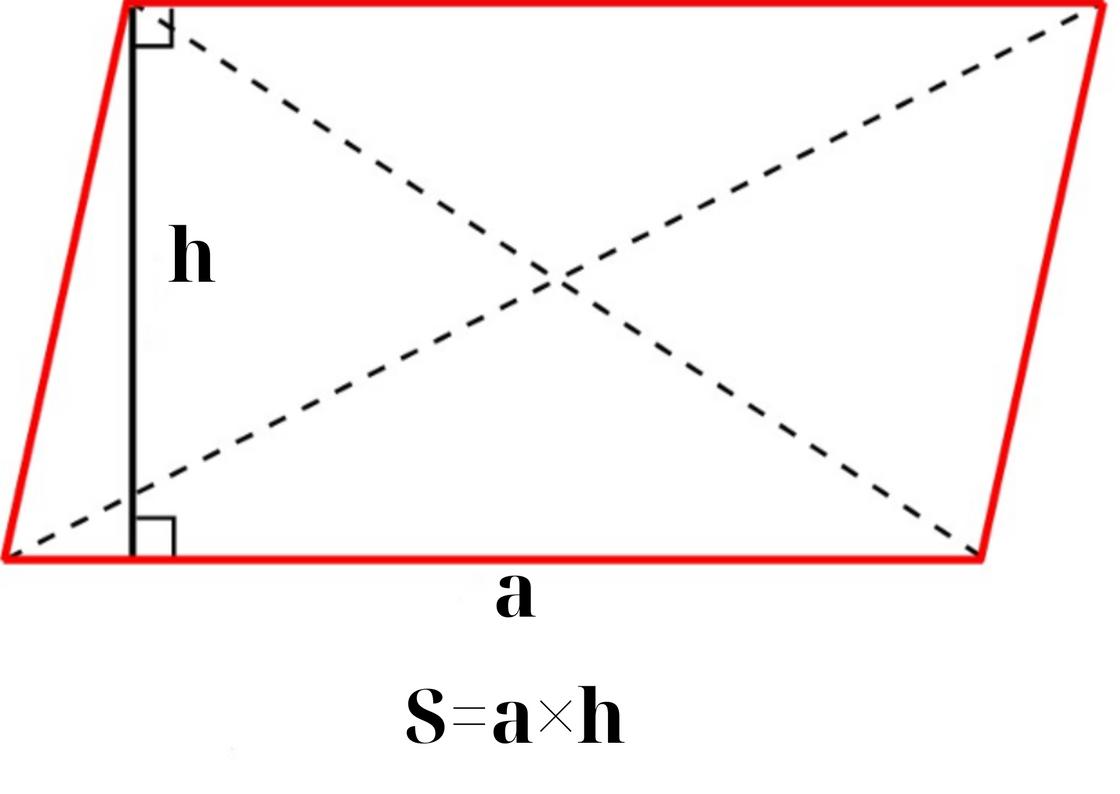
Параллелограмм — это четырёхугольник, у которого противоположные стороны параллельны друг другу, равны между собой и соединены под разными углами. Площадь такой фигуры равна произведению основания на её высоту: S=a×h, где a — основание, h — высота. При этом берётся то основание, на которое опускается высота из одного из углов. Например, основание a=8 см, высота h=5 см, тогда площадь S=8×5=40 см².
Наглядное обоснование правильности такого способа даёт обучающая платформа Splash Learn. Ресурс предлагает вырезать из бумаги параллелограмм, провести высоту и отрезать треугольник, который она образовала. Если этот треугольник приставить к другой стороне параллелограмма, то получится прямоугольник, для которого верна формула площади, как произведение его сторон.
Параллелограмм, у которого все стороны равны, называется ромб. Площадь ромба равна половине произведения его диагоналей: S=d1×d2÷2, где d1 и d2 — диагонали. Если d1=3 см, d2=6 см, то площадь такого ромба S=3×6÷2=9 см².
Площадь трапеции
Трапеция — это четырёхугольник, у которого две стороны параллельны (называются основаниями), а две боковые — разные. Трапеции бывают с разными сторонами, равнобокими (если боковые стороны равны), прямоугольными (если одна из боковых сторон перпендикулярна основаниям).
Как найти площадь трапеции? Площадь трапеции равна половине суммы оснований, умноженной на высоту: S=(a+b)÷2×h, где a и b — основания, h — высота. В равнобоких трапециях или с разными сторонами высоту проводят на большее основание. В прямоугольной трапеции высотой будет считаться сторона, перпендикулярная основаниям.
Например, в задаче даны такие размеры геометрической фигуры: a=10 см, b=6 см, h=8 см. Площадь такой трапеции вычисляется так: S=(10+6)÷2×8=16÷2×8=64 см².
Площадь треугольника
Треугольники создают три отрезка ломаной линии, которые соединяются в трёх вершинах. Эти геометрические фигуры бывают:
- разносторонними (все стороны разной длины);
- равносторонними (стороны одинаковой длины);
- равнобедренными (две стороны равны);
- прямоугольными (две смежные стороны сходятся под прямым углом).
Как найти площадь треугольника? Для вычисления площади треугольника надо знать одну из его сторон и высоту, которая проведена на неё как на основание. Тогда площадь фигуры равна половине произведения основания на высоту: S=(a×h)÷2, где a — основание, h — высота. Например, если для разностороннего, равностороннего или равнобедренного треугольника дана высота h=7 см, основание а=10 см, то площадь S=(7×10)÷2=70÷2=35 см².
В прямоугольном треугольнике две стороны соединены под прямым углом 90° и называются катетами. Тогда один из его катетов (а) можно считать основанием, а второй (b)— высотой, проведенной на основание. Площадь такого треугольника равна половине произведений его катетов: S=(a×b)÷2. Например, если а=8 см, b=5 см, то S=(8×5)÷2=20 см².
Площадь круга
Круг — это геометрическая фигура, которую создает замкнутая кривая линия, а все её точки находятся на одинаковом расстоянии от центра, а граница круга — это окружность. То есть круг — это часть плоскости внутри окружности. У окружности есть радиус (расстояние от центра до любой точки окружности) и диаметр (соединяет две точки на окружности и проходит через её центр). Диаметр равен двум радиусам.
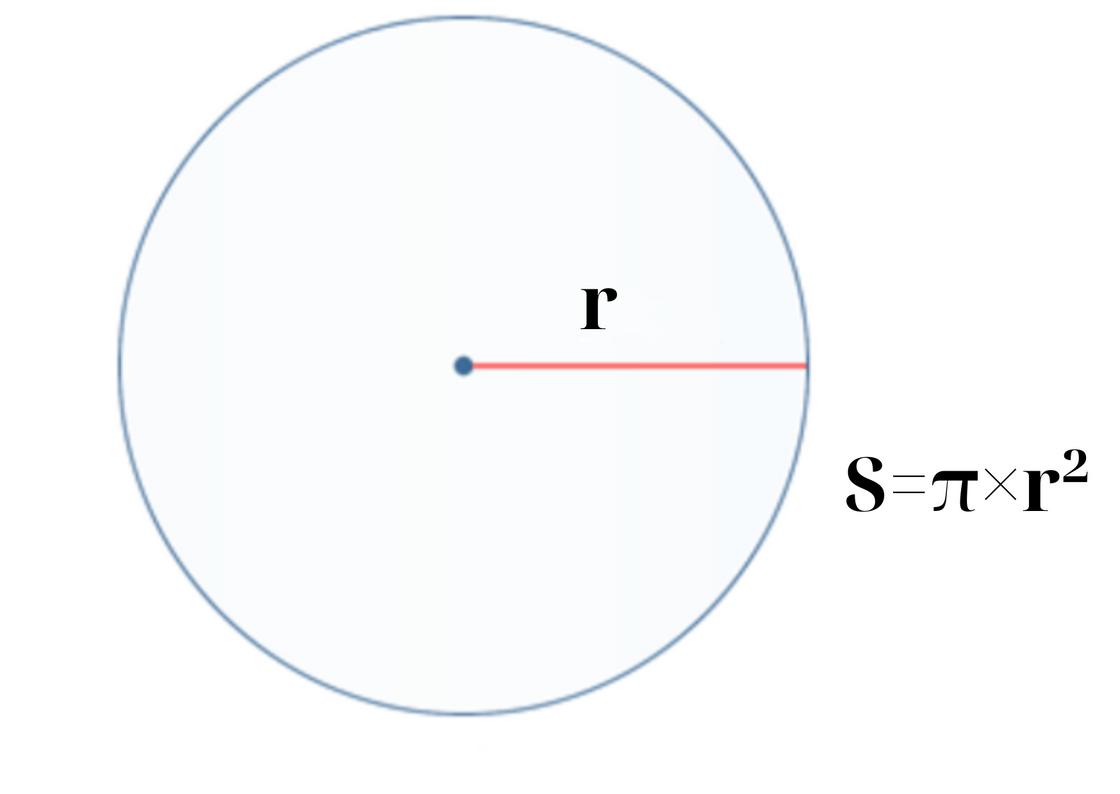
Площадь круга можно вычислить с помощью радиуса (r), диаметра (d), а также числа π. Число π — это константа (постоянная величина), которая равна отношению длины окружности к диаметру, π всегда равна 3,14. Формулы для этих вычислений выведены такие:
- Если дан радиус, площадь круга равна произведению π на квадрат радиуса: S=π×r². Например, при r=5 см площадь S=3,14×5²=3,14×25=78,5 см².
- С помощью диаметра площадь круга вычисляется по формуле S=πd²÷4. Так, если дан d=10 см, то площадь S=3,14×10²÷4=3,14×100÷4=78,5 см².
Иногда надо вычислить площадь круга по известной только длине его окружности, обозначаемой буквой L. В таком случае площадь круга вычисляется по формуле S=L²÷4π. Так, если L=40 см, то площадь круга S=40²÷(4×3,14)=1600÷12,56=20,09 см².
Формулы вычисления площадей предназначены для запоминания. Они станут базой для дальнейших, более сложных исчислений.

